Let us now see how the code for absolute value looks like in Matlab if we want to compute absolute value for an array of complex numbers. Z complex ab creates a complex output z from two real inputs such that z a bi.

How To Find The Modulus And Argument Of A Complex Number Youtube
The modulus of 3 2i is the square root of 3 2 2 2 13 so 3 2i 13 12.

Modulus of complex number matlab. We will follow the following 2 steps. To find the modulus for each coefficient of the polynomial a use ct coeffs a. With these we can define an auxiliary function that helps print out the magnitude and phase of a complex number in polar form.
Modulus of a complex number gives the distance of the complex number from the origin in the argand plane whereas the conjugate of a complex number gives the reflection of the complex number about the real axis in the argand plane. You can use them to create complex numbers such as 2i5. The complex plane has a real axis in place of the x-axis and an imaginary axis in place of the y-axis.
The complex magnitude or modulus is the length of a vector from the origin to a complex value plotted in the complex plane. For a complex value a b i is defined as a 2 b 2. For a complex value a b i is defined as a 2 b 2.
In MATLAB i and j represent the basic imaginary unit. Here x and y are real numbers. The complex magnitude or modulus is the length of a vector from the origin to a complex value plotted in the complex plane.
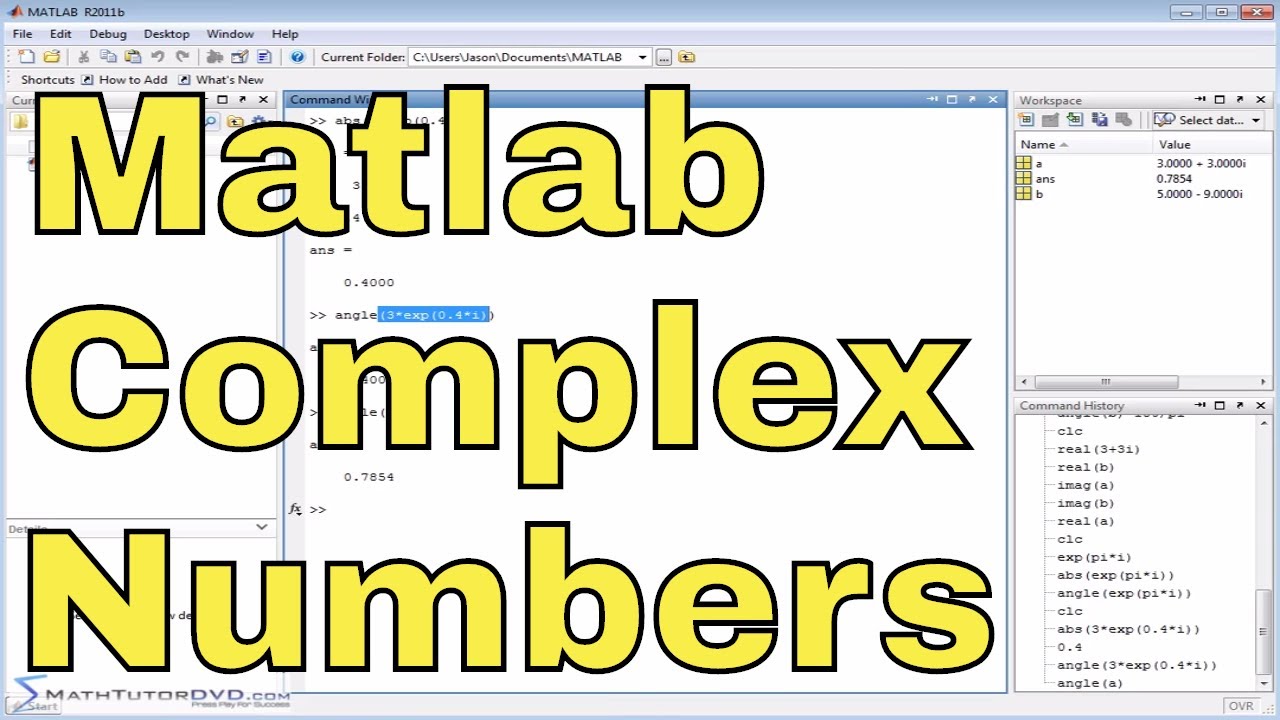
Use the MATLAB function abs to get the modulus of the complex number 3 2i. For example the max value is -0011523000474206i and the minimum value is 00026796 00006868i But if i give this command -0011523000474206i 00026796 00006868i it get. Learn how to use Complex Numbers functions in MATLAB.
It is independent of the positive or negative nature of the real and imaginary parts of the complex number. Ph angle z phase angle. In this example we will take an array of complex numbers and will find its absolute value using abs S function.
You can also determine the real and imaginary parts of complex numbers and compute other common values such as phase and angle. In this section we will discuss the modulus and conjugate of a complex number along with a few solved examples. Abs 3 2i Use the MATLAB function angle to get the argument of the complex number -1-i.
You can also determine the real and imaginary parts of complex numbers and compute other common values such as phase and angle. The file complexm is designed to be run in cell mode Open the file complexm in the Matlab editor then enable cell mode from the Cell Menu. To build on what Luis Mendo was talking about I dont believe there is a utility in MATLAB that prints out a complex number in polar form.
The absolute value of a complex number z x yi is the value z x 2 y 2. Since the complex number represented in MATLAB uses i as a symbolic character. The magnitude of the modulus is always a positive number.
Several modifications of the color scheme allow to incorporate additional information like the modulus of the function. After that use the entries on the Cell Menu or the icons on the toolbar to execute the code in the cells provided in the file. A and b are not double or single.
Where rho sqrtx2 y2 is the modulus of the complex number it can be obtained by setting absz while theta is its argument that is the angle between the x axis and the straight line issuing from the origin and passing from the point of coordinate x y in the complex plane theta can be found by typing angle. In MATLAB i and j represent the basic imaginary unit. M abs z magnitude.
Then continue with the normalization step. The absolute value of a complex number is also called a complex modulus. Create an array of complex number.
In Matlab complex numbers can be created using x 3 - 2i or x complex3 -2. Instead mod ab returns an unevaluated symbolic expression if a is a symbolic polynomial and b is a real number. The user must provide a field matrix of complex numbers z which covers the domain typically a rectangle a disk or an annulus of the function and a field of the same size with the corresponding values wfz.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features 2021. The modulus of z z conjugate and -z are equal. Vectors complexrandnkn randnkn.
There are options for executing both single and multiple cells. The complex function provides a useful substitute for expressions such as a 1ib or a 1jb when. Matlab Online Tutorial - 20 - Calculating the Magnitude and Angle of Complex Numbers.
You can use them to create complex numbers such as 2i5. You can now create periodic symbolic functions by defining the periodicity using mod. I have set that contain complex number then i get the greatest value using max function and get the smallest value using min function.
Heres a vectorized version of the normalization. The real part of a complex number is obtained by realx and the imaginary part by imagx. However we can use abs and angle to our advantage as these determine the magnitude and phase of a complex number.
Vectors bsxfunrdivide vectors sqrtsumvectorsconjvectors 2. Direct link to this answer. Matlab Online Tutorial - 20 - Calculating the Magnitude and Angle of Complex Numbers - YouTube.
B is all zeros.
Matlab Online Tutorial 20 Calculating The Magnitude And Angle Of Complex Numbers Youtube

Complex Numbers Modulusargument Form Modulusargument Form The Complex

Matlab Complex Numbers Representation Stack Overflow

Polar Form Of A Complex Number Math Methods Math Formula Chart Math Vocabulary
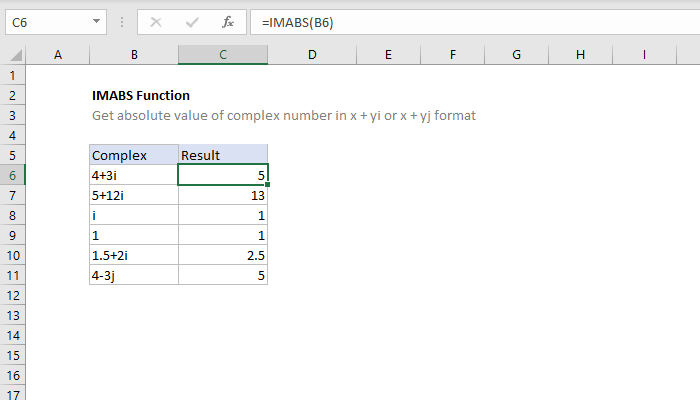
How To Use The Excel Imabs Function Exceljet