N ap A k bp B n-k cp C we get. Mathematically the modulo congruence formula is written as.

Shift Cipher Article Ciphers Khan Academy
Alternately you can say that a and b are said to be congruent modulo n when they both have the same remainder when divided by n.

K modulo p. P 1 k 1 p 2 k 2 p 3 k 3. Modulo p so altogether they produce a contribution of -1q modulo p. Stack Exchange network consists of 178 QA communities including Stack Overflow the largest most trusted online community for developers to learn share their knowledge and build their careers.
Find Square Root under Modulo p Set 2 Shanks Tonelli algorithm 22 Apr 16. So it is impossible when n is a prime for a quadratic like x2 1 to have more than 2 roots as we saw it having in mod 8 arithmetic. Interior designers in Bangalore.
Are integers greater than or equal to 1. Use the Chinese Remainder Theorem to show. Modular arithmetic is the arithmetic of remainders.
For example any solution to x3 x 3 0 mod 25 such as x 6 is also a solution to x3 x 3 0 mod 5. The group is cyclic if and only if n is 1 2 4 p k or 2p k where p is an odd prime and k 0For all other values of n the group is not cyclic. Note that a quadratic like x2 x1 in mod 2 arithmetic can have.
The idea is to find all primes smaller than n using Sieve of Eratosthenes. Note that this is different from. Thus t 0 and n 0 mod p n1.
You want to calculate n. Not rarely in combinatoric problems it comes down to calculating the binomial coefficient n choose k for very large n andor k modulo a number m. The above expression is pronounced is congruent to modulo.
Conversely if n p 1sthen g gp 1 s 1s 1 mod p. Both n and k modulo p are 0 in this case and theres a specific point in ChooseModTwo where this causes the output of the program to be 0. What is the range of p.
More explicitly if we rst. The units modulo p and so this contradicts our assumption that gis a primitive root modulo p. The problem here is that factorials grow extremely fast which makes this formula computationally.
When we have both of these we call congruence modulo. For every prime p i find the largest power of it that divides n. Compute p i k i p using.
For the second part the rst condition is equivalent to gj k 1 mod p by multiplying by g. Are primes and k 1 k 2 k 3. Bmod p without taking all the multiple factors of p into account that appear in the factorial.
Is the symbol for congruence which means the values and are in the same equivalence class. So it is in the equivalence class for 1 as well. May 29 14 at 1921.
So if we write. Show that primitive roots dont exist modulo any number of the form pqfor distinct odd primes p q. The multiplicative group F p of nonzero congruence classes modulo p is a cyclic group.
Maximum subarray sum modulo m. Theorem 1 Let n N. We KPC Modular Designers started in the years 2008 are one of the foremost manufacturers of an extensive array of Furniture.
Congruence Modular Arithmetic 3 ways to interpret a b mod n Number theory discrete math how to solve congruence Join our channel membership for. For each odd prime p we conjecture the distribution of the p-torsion subgroup of K 2n O F as F ranges over real quadratic fields or over imaginary quadratic fieldsWe then prove that the average size of the 3-torsion subgroup of K 2n O F is as predicted by this conjecture. For some k Z.
Where By definition the group is cyclic if and only if it has a generator g a generating set g of size one that is the powers give all possible residues. A b mod n and n is called the modulus of a congruence. Our offered range consists of best grade Wooden Cupboard Modern Kitchen and Office Furniture.
Cyclic Redundancy Check and Modulo-2 Division. Then congruence modulo n is an equivalence relation on Z. Roots of a Polynomial Theorem 2 When n is prime number then a polynomial of degree k say a0 a1xa2x 2 a kx k 0 mod n with ai 012n1 has at most k solutions.
The order of F p is p 1 so a primitive element is a nonzero congruence class whose order in F. Then a primitive root mod nexists if and only if n 2 n 4 n pk or n 2pk where pis an odd prime. The Multiplicative Group of Integers modulo p Theorem.
Stack Exchange network consists of 178 QA communities including Stack Overflow the largest most trusted online community for developers to learn share their knowledge and build their careers. Tells us what operation we applied to and. P is a constant 1000003.
Primitive root of a prime number n modulo n. Where p 1 p 2 p 3. In general the binomial coefficient can be formulated with factorials as n choose k fracnkn-k 0 leq k leq n.
Each of the full runs jp k 1 k p is congruent to p-1. A generator for this cyclic group is called a primitive element modulo p. Find sum of modulo K of first N natural number.
Our first result concerning congruences should be familiar from Intro to Abstract. Thus formally the task is. The second condition is equivalent to j.
Two numbers a and b are said to be congruent modulo n when their difference a - b is integrally divisible by n so a - b is a multiple of n. Modulo p simply by considering it modulo p. And subsequent terms will reduce to zero but in fractions all multipliers containing p can be reduced and the resulting expression will be non-zero modulo p.
A primitive root modulo nis an integer gwith gcdgn 1 such that ghas order n. The last possibly incomplete run produces r. This was first proved by Gauss.
Our basic idea is that this procedure can also be run in reverse by rst nding all the solutions modulo p and then using them to compute the solutions modulo pd. May 29 14 at 1919. This means that for these n.
Let the largest power be k i. Let p be a prime integer. For the numbers coprime to p we will only be interested in the contribution modulo p.
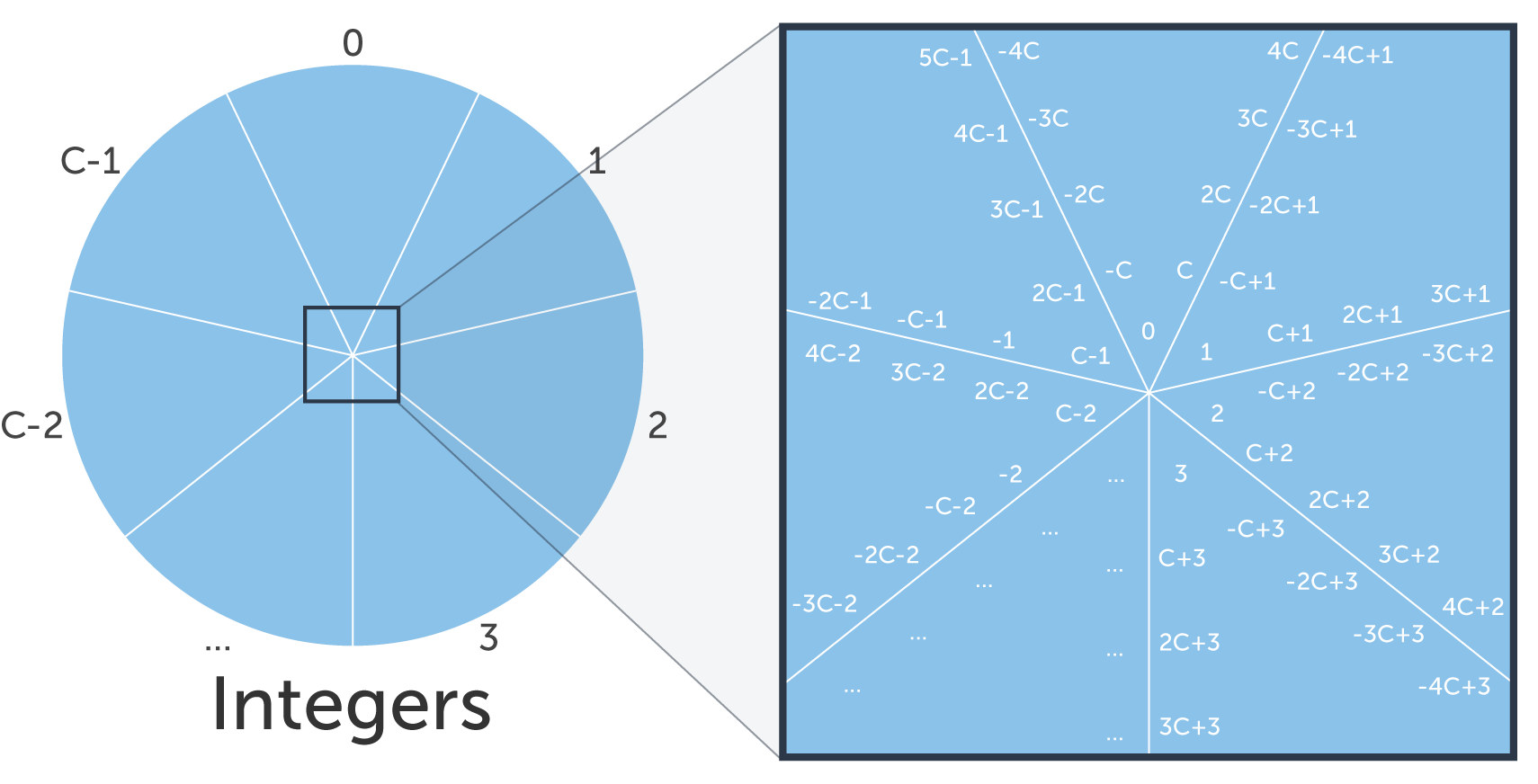
Congruence Modulo Article Cryptography Khan Academy

Modular Arithmetic This Lecture Modular Arithmetic Is An
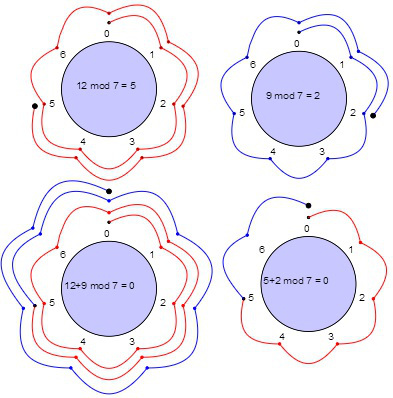
Modular Addition And Subtraction Article Khan Academy

Computational Complexity Of Modular Exponentiation From Rosen S Discrete Mathematics Mathematics Stack Exchange

Modular Arithmetic This Lecture Modular Arithmetic Is An

Modular Arithmetic This Lecture Modular Arithmetic Is An