Modulus Of Complex Number 3i-4 Is

Saturday, February 6, 2021

By decomposing the number inside the radical we get 5 5 5. ExampleFind the modulus and argument of z 43i.

Modulus Of A Complex Number Definition Examples Video Lesson Transcript Study Com

23i 2232 49 13.

Modulus of complex number 3i-4 is. So if the number is 4 3i. Z a bi zcosθisinθ z a b i z cos θ i sin θ The modulus of a complex number is the distance from the origin on the complex plane. Modulus of complex number v v zw zw 513 65.

This is called the triangle inequality which is true for complex numbers and can be visualized in the same way. The modulus of z is the length of the line OQ which we can. Find the modulus and amplitude of the following complex numbers.

For example the modulus of the complex number. Now we apply the formula of modulus of complex number Z. Find the modulus and argument of the following complex numbers and hence express each of them in the polar form.

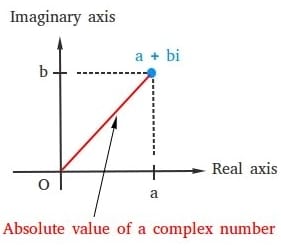
The modulus of 3 4i is 5. Question Bank Solutions 5552. The absolute value or modulus is the distance of the image of a complex number from the origin in the plane.

In the complex number 3 4i a 3 and b 4. The absolute value or modulus is the distance of the image of a complex number from the origin in the plane. Z 4 3i z - 4 - 3 i.

Find the modulus and argument of a complex number - Examples. This will be the modulus of the given complex number. Z a 2.

It has been represented by the point Q which has coordinates 43. Be a complex number. The modulus of complex number z a b i is.

It is to be noted that the conjugate complex has a very peculiar property. Square of Real part x 2 Square of Imaginary part y 2. Find the modulus of the following complex number.

Then OP z x 2 y 2. What is the modulus of a complex number. To find the modulus of 3 4i we can use our modulus formula.

Hope u got it if there is mistake in question let me know it. Z a b i a b i z a 2 b 2. If we multiply a complex number by its complex conjugate think about what will happen.

R cos θ i sin θ Here r stands for modulus and θ stands for argument. We alter the sign of the imaginary component to find the complex conjugate of 4 3i. Modulus of Complex Number.

12i1-3i asked Jun 13 in Complex Numbers by Labdhi 312k points complex numbers. Z b 3. Modulus of the complex number is the distance of the point on the argand plane representing the complex number z from the origin.

Maharashtra State Board HSC Science General 11th. Z z z. Modulus of complex number 1 2i-2 3i is 65.

Formula for modulus of complex number aib is a2 b2 under root a square plus b square. Answered 5 years ago Author has 62 answers and 1222K answer views. Observe now that we have two ways to specify an arbitrary complex number.

4 4i. 2 3i 4 9. 2 3i 13.

This is the trigonometric form of a complex number where z z is the modulus and θ θ is the angle created on the complex plane. Misc 13Find the modulus and argument of the complex number 1 2i1 3i. Put the value of a and b in the above formula.

One is the standard way x y which is referred to as the Cartesian form of the point. The calculator uses the Pythagorean theorem to. The complex number z.

Advertisement Remove all. The absolute value of a complex number abi also called the modulus is defined as the distance between the origin 00 and the point ab in the complex plane. Then the modulus of a complex number Z denoted by Z is defined to be the non-negative real number Z Re.

W -2 2 3 2 4 9 13. To find the modulus of a complex number you find the distance the complex number is from the center of the complex plane using the distance formula. Multiply the second term of the first parentheses by the first term of the second parentheses.

Then the modulus 42 32. Multiply the second term of the first parentheses by the second term of the second parentheses. 2 3i is.

SolutionThe complex number z 43i is shown in Figure 2. In this case z 4 3 i so its modulus is. 2 3i 22 32.

The calculator uses the Pythagorean theorem to. Z 4 2 3 2 25 5. Let P is the point that denotes the complex number z x iy.

The second is by specifying the modulus and argument of z instead of its x and y components ie in the form. To find the modulus and argument for any complex number we have to equate them to the polar form. Let z 4 3i z 4 3i z 4 2 3 2 16 9 25.

2 3i 2 - 02 3 - 02. Write all the terms. Find the modulus and amplitude of 4 3i.

First we solve 1 2𝑖1 3𝑖 Let 𝑧 1 2𝑖1 3𝑖 Rationalizing the same 1 2𝑖1 3𝑖 x 1 3𝑖1 3𝑖 1 2𝑖 1 3𝑖1 3𝑖 1. Z 2 a 2 b 2. If your sums are infinite then the inequality still holds since the partial sums on the left are less than or equal to those on the right so the limits also satisfy this inequality.

Concept Notes Videos 418 Syllabus. Add up the terms. Find the square root of the computed sum.

Modulus of a complex number is the distance of the complex number from the origin in a complex plane and is equal to the square root of the sum of the squares of the real and imaginary parts of the number. Let us look into the next example on How to find modulus of a complex number. So the complex conjugate is 4 3i.

Misc 13 - Find modulus argument of 1 2i1 - 3i - Miscellaneous. Find the sum of the computed squares. Sum Square of Real part Square of Imaginary part x 2 y 2.

Let us see some example problems to understand how to find the modulus and argument of a complex number. The modulus and argument are fairly simple to calculate using trigonometry.

Modulus And Conjugate Of A Complex Number Absolute Value Examples