Module 6 Torsion Learning Objectives 61 Formulation of the basic equations of torsion of prismatic bars St. In the steel Sections tables ie BS EN 10210-2.

Torsional Equation Torsional Formula Torsion Strength Of Materials Youtube
Venant torsional constant J measures the resistance of a structural member to pure or uniform torsion.

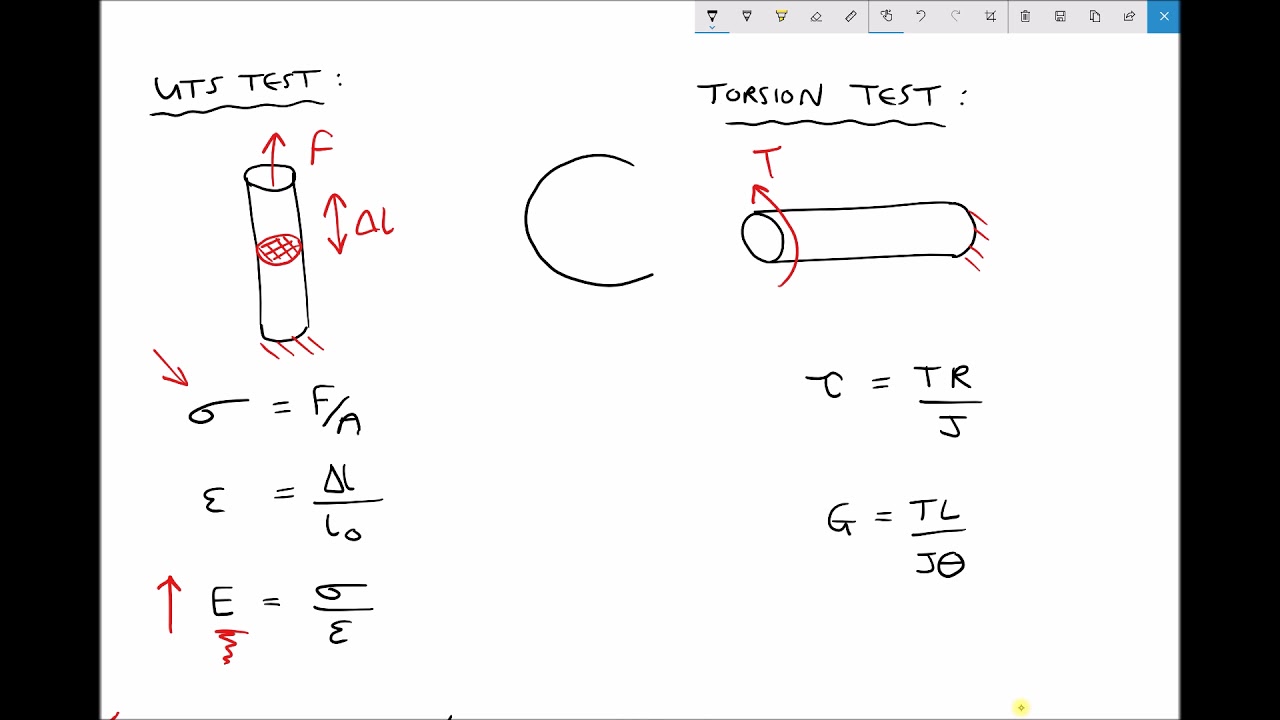
Torsion modulus j. L Length of the shaft. SinceinthesimpletwistingcaseunderconsiderationthequantitiesTJGareconstant alongztheangleoftwistcanbewrittenas d dz constant L TL GJ 13 Thisisanalogoustotheexpression PLAEfortheelongationofauniaxialtensile specimen. It is used in calculating the buckling moment resistance of laterally unsupported beams and torsional-flexural buckling of compression members in accordance with.
ZGr d dz Gr L Gr L TL GJ z. G Shear modulus or modulus of rigidity. For a given shaft I P and R are constants and I P R is thus a constant and is known as POLAR MODULUSZ P.
J π D432 This first equation can be rewritten in the form of angular displacement modulus of rigidity and length of shaft and follow. Thus the SI unit for torque is Nm. In the simplest of terms it is the resistance to twist.
From the relation TJ τR. We have T τJR τZ P. In structural steel design the Torsion Constant J represents the ability of the steel beam to resist torsion ie.
Polar modulus of the section is thus measure of strength of shaft in torsion. The polar section modulus also called section modulus of torsion Z p for circular sections may be found by dividing the polar moment of inertia J by the distance c from the. J Polar moment of inertia.
Rotating Shafts and Torques - Torsional moments acting on rotating shafts. For this equation we should note that half the rod is solid the other half is hollow which affects how we calculate J for each half. The SI unit of torque is depended on the SI unit of force which is Newton N and the SI unit for distance which is meter m.
Assume the modulus of rigidity for steel is 80 GNm2. The Torsion constant J for Hollow Rolled Sections are calculated as follows. J 2I For square and rectangular hollow sections.
Sadd 93 Timoshenko Chapter 11 e 2 e 1 e 3 Figure 61. GθLJ substituting for the polar moment of inertia TJ τr GθL. These are the steps followed to derive the torsion equation.
Modulus of elasticity of steel 29000 ksi warping constant for the cross-section in4. Theta Twist angle. So we need to consider our deformations for torsion that means lets turn to our equation that describes the superposition of twist angles.
Where T is the applied torque c is the radius and J is the polar moment of the cross-sectional area. Tau Shear stress at a radial distance of R. τr Gθl In above equation G is the modulus of rigidity l is the length if the shaft and θ is the angular displacement as a result of applied torque.
All torsion problems that you are expected to answer can be solved using the following formula. When torsion must be resisted by the member directly its effect may be reduced through consideration of intermediate torsional support provided by secondary framing. A hollow steel shaft with a diameter ratio of 075 and a length of 4 m is required to transmit 1 MW at 120 revmin.
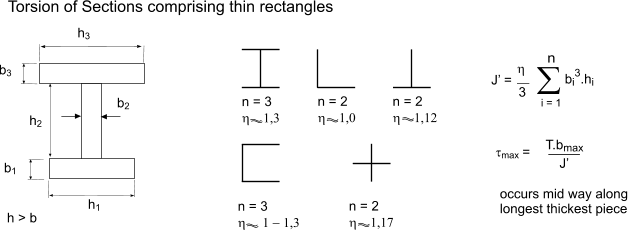
For a solid circular member. J 13 t 3 h 2k A h where. Torsion of a prismatic bar We will employ the semi-inverse method that is we will make assumptions as to the 125.
Torsion is the action of twisting on an object or in relation to another. On the surface of a circular torsion member Figure 1 the state of shear stress in the axial and circumferential directions is given by. The modulus of rigidity shear modulus is the unit of measure of the force required to deform an object along its axis.
T Torque or Torsion. 2 may be computed approximately from dz T JG d sv φ Version II 17-4. This process is also termed as the derivation of the torsion equation for a circular shaft.
I is the second moment of area t is the thickness of section h is the mean perimeter 2 B - t D - t - 2 R c 4 -. This equation is called Torsion equation. 241 Torsional Constant J for thin walled open sections made up of rectangular elements Torsional Constant J for members made up of rectangular plates see Fig.
Stress - Stress is force applied on cross-sectional area. T torque or twisting moment Nm lbin J polar moment of inertia or polar second moment of area about shaft axis m 4 in 4 τ shear stress at outer fibre Pa psi r. Similar to the modulus of elasticity E for a body under tension a shaft in torsion has a property known as the shear modulus also referred to as the modulus of elasticity in shear or the modulus of rigidity.
For circular hollow sections. The product of the torsion constant Jt x G shear modulus gives you the torsional rigidity. The shear modulus G is the ratio of shear stress to shear strain.
Modulus of Rigidity - Shear Modulus Modulus of Rigidity is the elasticity coefficient for shearing or torsion force. Of the shaft section. Its units are mm 4 or inches 4.
Stiffness - Stiffness is resistance to deflection. 1997Hot finished Rectangular Hollow Sections BS EN 10219-2Cold Formed Circular Hollow Sections The Torsion Constant J and the Torsion modulus constant C are listed. J T The complete torsion equation is 25132 x 10 m 32 x 004 32 J 6 -9 max-9 4.
TJ τR GθL.
Determining Shear Strength And Modulus Of Rigidity For A Material Using Destructive Torsion Testing Youtube

Is It Possible To Calculate The Torsion Constant Of A Rod Given The Shear Modulus Moment Of Inertia And Length Physics Stack Exchange

Torsional Rigidity Versus The Shear Modulus Of Inclusion Download Scientific Diagram
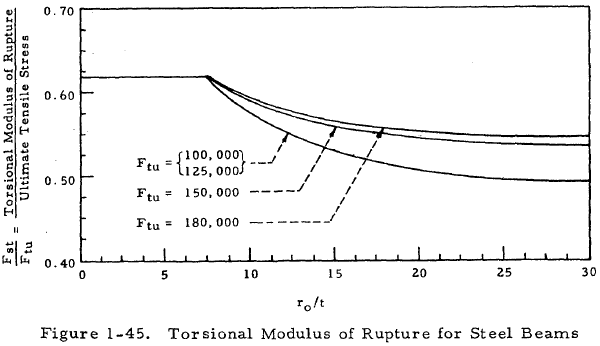
Beam Torsion Engineering Library