-5 6 2 3 9 which is a. A mod b r.

Mod Counters Are Truncated Modulus Counters
Remainder of 2155 15 Remainder of 10055 10 Remainder of 11999999999999993 Remainder of 4317 10.
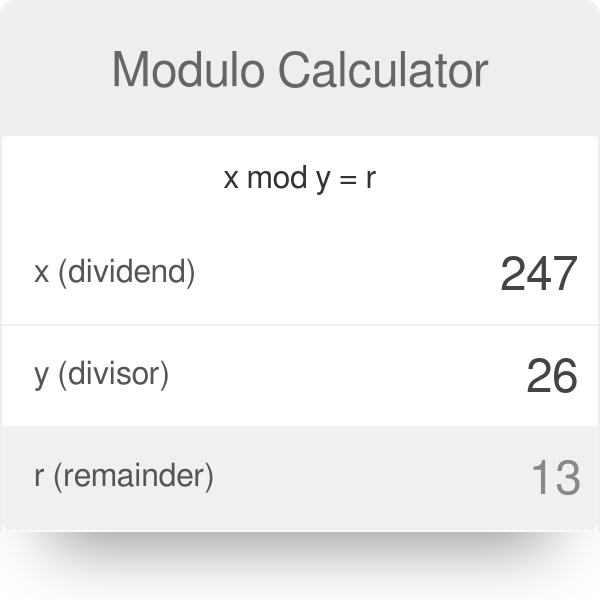
2^n modulo 5. 11 mod 4 3 because 11 divides by 4 twice with 3 remaining. Two numbers a and b are said to be congruent modulo n when their difference a - b is integrally divisible by n so a - b is a multiple of n. A b 1 thus only the value of u u is needed.
Using the Chinese remainder theorem the problem is reduced to the case of a prime power p n. The modulo operator denoted by is an arithmetic operator. First we know that m 5 so 2 n must be greater than 5.
-2 -1 0 1 2 Naturally it is normal to express such sets in a logical fashion as in 52 but any representative of the respective residue class could be used. How to calculate a modular inverse. We rst show that no two of 012n 1 are congruent modulo n.
More generally the set a Z. The set 515 from above for example is an instance of a reduced residue system modulo 4. About Modulo Calculator.
The modulo division operator produces the remainder of an integer division. This free easy-to-use Modulo Mod Calculator is used to perform the modulo operation on numbers. Suppose we want to design a MOD-5 counter how could we do that.
Given the Eulers totient function φn any set of φn integers that are relatively prime to n and mutually incongruent under modulus n is called a reduced residue system modulo n. In writing it is frequently abbreviated as mod or represented by the symbol. Addition of congruence classes modulo N is defined by choosing any element from each class adding the elements together and then taking the congruence class modulo N that the sum belongs to as the answer.
3 2 1 - 5 4 2 - 1 4 6 7. 181 rows In computing the modulo operation returns the remainder or signed remainder of a division. Here the gcd value is known it is 1.
A n2 n2 is a complete system of residues modulo n. If n 2 q 3 r 5 s 17 t where r 2 s 2 and t 2 the program can find the roots as radical expressions. ModularArithmetic One of the facts that makes congruences so useful in arithmetic is.
Then t s is a positive integer and t s n. A b mod n and n is called the modulus of a congruence. Mathematically the modulo congruence formula is written as.
N 1 by Z n. Alternately you can say that a and b are said to be congruent modulo n when they both have the same remainder when divided by n. We may omit mod n when it is clear from context.
Given two numbers a the dividend and n the divisor a modulo n abbreviated as a mod n is the remainder from the division of a by nFor instance the expression 7 mod 5 would evaluate to 2 because 7 divided by 5 leaves a remainder of 2 while. The numeric arguments are first converted to a common type. Modulo is a math operation that finds the remainder when one integer is divided by another.
Namely 0 n 1 n 2 n n 1 n. If x and y are integers then the expression. You may also enter the math expression containing other integers and the.
For irreducible polynomials of the form a x n b the roots can be computed as the product of a real number by a complex root of 1 so the method used in the previous paragraph is used. B modam returns the remainder after division of a by m where a is the dividend and m is the divisorThis function is often called the modulo operation which can be expressed as b a - mflooramThe mod function follows the convention that moda0 returns a. Solving the quadratic congruence x 2 a mod m This works for m with up to say 20 digits due to the limitations of the program used to factor m.
This modulo calculator performs arithmetic operations modulo p over a given math expression. Where a is the dividend b is the divisor or modulus and r is the remainder. For two integers a and b.
Congruence Modular Arithmetic 3 ways to interpret a b mod n Number theory discrete math how to solve congruence Join our channel membership for. To calculate the value of the modulo inverse use the extended euclidean algorithm which find solutions to the Bezout identity aubv GCDab a u b v GCD. We denote the set 0.
Thus one possible system for arithmetic modulo 5 would be 2 1 0 1 2. The next set is also a complete residue system modulo 5 using the least absolute values modulo 5. The set of all congruence classes of the integers for a modulus n is called the ring of integers.
This example uses negative numbers with the modulus operator. Using negative numbers with modulus operator. There are exactly n distinct congruence classes modulo n.
Let n be a positive integer. Thus n does not. As 2 1 2 2 2 4 2 3 8 and 8 is greater than 5 then we need a counter with at least three flip-flops N 3 to give.
Take a step-up from those Hello World programs. The modulo operator yields the remainder from the division of the first argument by the second. To see this suppose that 0 s t n.
Modulo Operator in CC with Examples. This is based on operator precedence. System of residues modulo n by Theorem 2.
While you still can simply enter an integer number to calculate its remainder of Euclidean division by a given modulus this modulo calculator can do much more. The set 012 is a complete system of residues modulo 5. We consider two integers x y to be the same if x and y differ by a multiple of n and we write this as x y mod n and say that x and y are congruent modulo n.

Mod Counters Are Truncated Modulus Counters

Mod Counters Are Truncated Modulus Counters

Mod Counters Are Truncated Modulus Counters
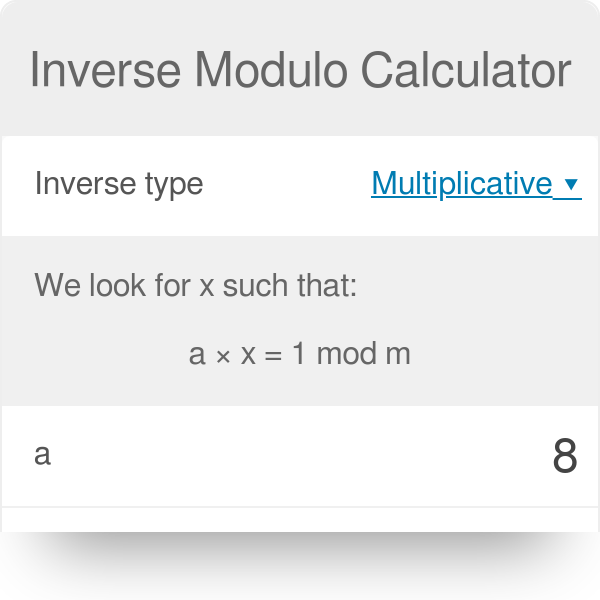
Inverse Modulo Calculator Definition Examples

Multiplication Modulo Example Youtube
