Heres what I have done. Given two positive numbers a and n a modulo n abbreviated as a mod n is the remainder of the Euclidean division of a by n where a is the dividend and n is the divisorThe modulo operation is to be distinguished from the.

Pdf On Modulo 2 N 1 Adder Design Semantic Scholar
Multiplying 74 by 7 the modulus of 75 and multiplying 75 by 5 the modulus of 74.
N modulo 2 arithmetic. Taking m 2 every integer is congruent modulo 2 to exactly one of 0 and 1. Find the remainder when N is divided by 36. In computing the modulo operation returns the remainder or signed remainder of a division after one number is divided by another called the modulus of the operation.
Then 0 42024 the set of even integers. Congruence is an equivalence relation if a and b are congruent modulo n then they have no difference in modular arithmetic under modulo n. Use modulo-2 binary division to divide binary data by the key and store remainder of division.
We discussed in class number theory and after making some proofs on division algorithms we made some modular arithmetic. Note that the congruence class a is a set of integers. Therefore N 123456789101112131435.
Randolph High School Math League 2014-2015 Page 4 Solution. Congruence Modular Arithmetic 3 ways to interpret a b mod n Number theory discrete math how to solve congruence Join our channel membership for. 2N mod 5 74 6N mod 7 75 We can make the two moduls the same mod 35 using the above Factors and Products theorem.
Each digit is considered independently from its neighbours. We have the congruences. To find b mod n the students should divide b by n and take the remainder as the answer.
Ab mod p a mod p b mod p mod p For example a 50 b 100 p 13 50 mod 13 11 100 mod 13 9 50 100 mod 13 50 mod 13 100 mod 13 mod 13 or 5000 mod 13 11 9 mod. So if I were to have for example 27 added to 8 modulo 32 I would have something like 27 8 mod 32 35 mod 32 3. Sometimes we are only interested in what the remainder is when we divide by.
In the following problems they are to find what number mod 2 is congruent to the given number. Solve 3x 2 0 mod 11 5. For these cases there is an operator called the modulo operator abbreviated as mod.
They are usually not congruent to their positive counter parts as you can see in the above examples. Because you know that n2 is the modulus you can just compute a real-valued square root of n2 and get n back. Append the remainder at the end of the data to form the encoded data and send the same Receiver Side Check if there are errors introduced in transmission Perform modulo-2 division again and if the remainder is 0 then there are no errors.
In modulo-2 arithmetic we use the ______ operation for both addition and subtraction. 217 Example Let n 2. All the other numbers can be found congruent to one of the n numbers.
We add r redundant bits to each block to make the length n k r. It is my understanding that the definition of addition modulo 2 32 is. Therefore the distinct elements of ZnZare 0.
24 mod 2 0 mod 2. The resulting n-bit blocks are called _________. Now you have effectively halved the length of the modulus.
AdditionSubtraction Modulo 2 additionsubtraction is performed using an exclusive OR xor operation on the corresponding binary digits of each operand. Solve 5x 4 mod 6 4. Numbers are not carried or borrowed.
We write a instead of an unless we are working modulo two different bases. In this work by taking advantage of the properties of modulo 2n-2 arithmetic we propose efficient modulo 2n-2 multi-operand adder multiplier as well as squarer architectures. Below is the fundamental modular property that is used for efficiently computing power under modular arithmetic.
Show activity on this post. Saying n 0 mod 2 means n 2kfor some integer k so nis even and saying n 1 mod 2 means n 2k 1 for some integer k so nis odd. They are to find what the number is modulo 2.
Find the least positive value of x such that i 71 x mod 8 ii 78 x 3 mod 5 iii 89 x 3 mod 4 iv 96 x7mod 5 v 5x 4mod 6 2. Ad Try this engaging resource in your classroom today. When we divide two integers we will have an equation that looks like the following.
Introduce the notation a b mod n to mean that b is the remainder when a is divided by n. A n b a b mod n. We seek the value of this number N.
In particular every a is congruent to its remainder when divided by n and no two distinct remainders are congruent modulo n. Suppose a number say N when divided by 5 leaves a remainder 2 and when divided by 7 leaves a remainder 6. An Introduction to Modular Math.
Because of this in modular n arithmetic we usually use only n numbers 0 1 2 n-1. Modulo 2 Arithmetic Modulo 2 arithmetic is performed digit by digit on binary numbers. Therefore power is generally evaluated under modulo of a large number.
Then a b mod n iff a and b leave the same remainder when divided by n. N 1 mod 2 N 0 mod 3 N 1 mod 4 N 0 mod 9. Let N be the integer of putting all natural numbers from 1 to 35 together.
Also note that if you can factor the modulus and recover p and q you can use the Chinese Remainder Theorem to split the discrete logarithm problem of n into two half-sized ones for p and q which is much. Ad Try this engaging resource in your classroom today. 1 31135 the set of odd integers.
Theorem 2 Let n Nand ab Z. Note that N can be written more mathematically as N a 0 10n a 1 10n 1 a 2 10n 2 a n 1 10. If x is congruent to 13 modulo 17 then 7x - 3 is congruent to which number modulo 17.

Does The Integers Modulo N With The Addition Modulo N Form A Commutative Group Of Size N Mathematics Stack Exchange

Lecture On Modulo Arithmetic Part 2 Youtube

Chapter 2 Parity Checks Simple Codes Modular Arithmetic Ppt Download
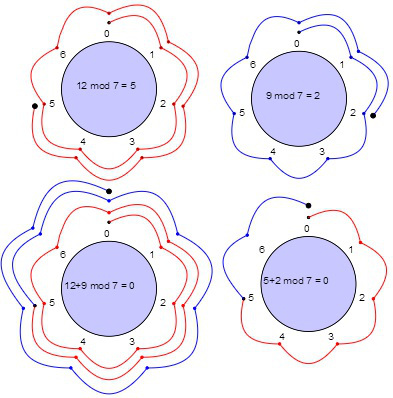
Modular Addition And Subtraction Article Khan Academy
Signed Lsb Representation Of Modulo 2 N 1 Residues Download Scientific Diagram

Coe 341 Data Computer Communications T 081 Dr